|
Gitter
Aus der Schule kennen wir Funktionen, die für alle reellen Zahlen definiert sind. Der Rechner
kann aus Rechenzeit- und Speicherplatzgründen die Lösung eines Problems im interessierenden Rechengebiet - z.B. die Temperaturen in der
Erdatmosphäre - nur an wenigen, endlich vielen Punkten bestimmen. Wir müssen daher eine Auswahl an Punkten im Rechengebiet vornehmen, nur an
diesen ermittelt man die interessierenden Größen. Die Anordnung dieser Punkte nennt man Gitter.
Auf den nächsten Seiten werden wir einfache eindimensionale Probleme betrachten. Wir benötigen dafür auch eindimensionale Gitter.
Zuerst wird also ein eindimensionaler Gegenstand, ein Stab bzw. eine Luftsäule, diskretisiert. D.h. ein Gitter wird aufgebaut, dessen Punkte sich
auf eine Raumkoordinate verteilen.
Der Stab bzw. die Luftsäule hat eine Länge, diese sei in x-Richtung orientiert.
Bild des Stabes
Ein sehr einfaches Programm zur Berechnung der Verteilung der Gitterpunkte auf diesen Stab wird im folgenden vorgestellt.
Die vom Programm ausgegebene Gitterdatei muß mindestens die Ortskoordinaten der Punkte enthalten.
Da sehr oft auch der jeweilige Abstand zwischen zwei benachbarten Punkten gebraucht wird, werden diese auch in die Gitterdatei eingeschrieben.
Wir nennen diesen Gittertyp FDM-Gitter, "FDM" wie "Finite Differenzen Methode", ein Verfahren um Differentialgleichungen und damit physikalische Probleme
zu lösen.
Dieser Gittertyp wird hier z.B. im Programm Absorption verwendet.
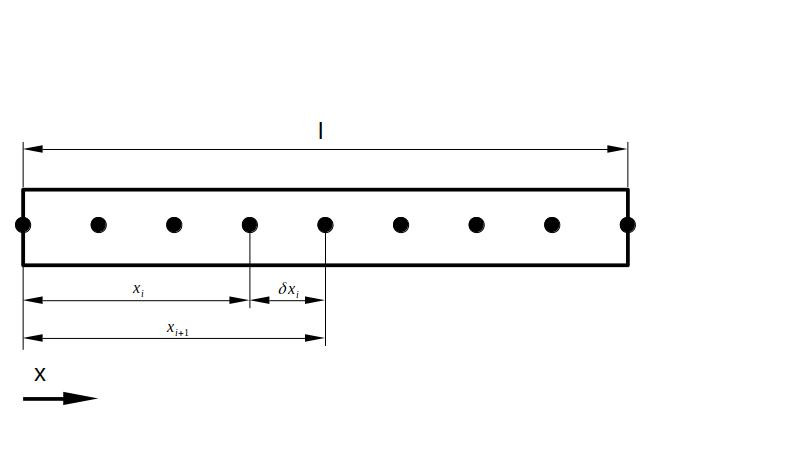
Stab mit FDM-Gitter
Bei einer oft angewandten numerischen Methode - der Methode der Finiten Volumen (FVM) - , welche die Flüsse einer Größe über
Grenzflächen von Teilvolumina bilanziert und somit die Werte dieser Größe errechnet, werden der Flächeninhalt und die Positionen
dieser Grenzflächen benötigt.
Ein FVM-Gitter ist untern dargestellt. Die Grenzflächen sind grün hervorgehoben. Die Finite Volumen Methode wird hier z.B. zur Lösung der
Wärmeleitungsgleichung verwendet.
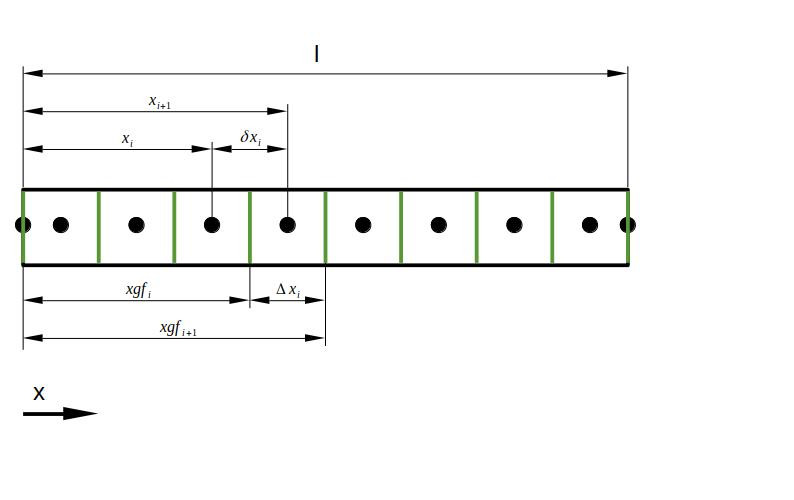
Stab mit FVM-Gitter
Das Programm liefert eine Datei, die Gitterdatei.
Anwenden des Programms
- Zuerst erstellen Sie ein Verzeichnis, in dem Sie das Programm "fluisa_gitter_1d" laufen lassen wollen.
- In diesem Verzeichnis benötigen Sie die Quelldateien, d.h. die python3-Dateien "fluisa_gitter_1d_haupt.py", "steuer.py", "gitterer.py" und
"ausgabe.py" sowie die Steuerdatei "steuer.txt".
- Am einfachsten ist es, das *.tar.gz-Archiv herunterladen und im Zielverzeichnis zu entpacken. Das können Sie z.B. mit dem Konsolenbefehl
tar -xzf fluisa_gitter_1d.tar.gz oder mit
einem Entpackprogramm wie Xarchiver machen. Das Archiv enthält die Quelldateien, die Steuerdatei und die Dokumentation des Programms als *.pdf.
- Sie können aber auch jede Datei einzeln herunterladen. Dann müssen Sie jeweils den Punkt - also "." - im Dateinamen vor py ergänzen.
Sie müssen die Dateinamen von "fluisa_gitter_1d_haupt.pytxt" in "fluisa_gitter_1d_haupt.py", "steuer.pytxt" in "steuer.py", "gitter.pytxt" in
"gitter.py" und "ausgabe.pytxt" in "ausgabe.py" ändern. Leider war es nicht möglich, die funktionierendem Dateiendungen beizubehalten, da
der Server eine Fehlermeldung beim Anklicken ausgibt.
Im *.tar.gz-Archiv sind alle Dateiendungen richtig, die Programme sind sofort nach dem Entpacken lauffähig.
- Dann öffnen Sie ein Konsolenfenster in diesem Verzeichnis (rechter Mausklick im Fenster des Verzeichnisses, dann
"Terminal hier öffnen" klicken).
- Führen Sie zur Sicherheit einen Virenscan über dieses Verzeichnis durch. Z.B. ich benutze clamscan mit dem Befehl
clamscan -r -i. Sie können natürlich einen anderen Virenscanner benutzen.
- Öffnen Sie die Steuerdatei steuer.txt mit einem Editor. Die Steuerdatei beinhaltet die Gitterparameter wie Anzahl der Punkte, Namen der
Ausgabedateien, Gittertyp. Besonders der Gittertyp (ob fdm oder fvm in der Datei) ist hier wichtig. Die auf der Website gespeicherte Steuerdatei erzeugt
ein Gitter wie das FDM-Gitter oben mit 9 Knotenpunkten.
- Dann wird das Programm gestartet:
- Das kann mit dem Konsolanbefehl python3 fluisa_gitter_1d_haupt.py geschehen.
- oder Sie starten die Python-Umgebung IDLE in der Konsole mit idle, öffnen die Datei "fluisa_gitter_1d_haupt.py" über den
Menüpunkt File -> Open.
Dann öffnet sich ein weiteres Fenster mit dem Hauptprogramm. Dieses wird dann mit dem Menüpunkt run module gestartet.
- Das Programm listet dem Benutzer die Steuerparameter, die in der Steuerdatei enthalten sind, auf und gibt dem Benutzer die Möglichkeit, die
Steuerdaten mit einem Klick auf den "Eingabe ändern"-Button zu ändern.
- Ein Klick auf den "weiter"-Button läßt das Programm das FDM-Gitter erstellen.
- Das Gitter wird als Graphik angezeigt, die Gitterwerte werden in einer Datei und als Graphik gespeichert.
- Ein Wegklicken der Graphik (großes Kreuz oben rechts) beendet das Programm.
Wie oben bereits beschrieben, können Sie die Steuerdaten ändern.
- Starten Sie das Programm erneut wie in Punkt 6.
- Klicken Sie auf den "Eingabe ändern"-Button.
- Dann erscheinen rechts von den Eingabedaten Eingabefelder, in die Sie die neuen Steuerdaten eingeben können.
- Wenn man in der Steuerdatei die Werte folgendermaßen ändert:
- Name der Gitterdatei: gitter_fdm_9.dat -> gitter_fvm_10.dat
- Name der Graphikdatei: gitter_fdm_9 -> gitter_fvm_10
- Anzahl der Gitterpunkte: 9 -> 10
- FDM- oder FVM- Gitter: d -> v
- und zuerst auf den "übernehmen"-Button, dann auf den auf den "weiter"-Button klickt, wird ein FVM-Gitter mit 10 Knotenpunkten erstellt.
- Das neue Gitter wird als Graphik angezeigt, die Gitterwerte werden in einer anderen Datei und als Graphik gespeichert.
- Ein Wegklicken der Graphik (großes Kreuz oben rechts) beendet das Programm.
Die FDM-Gitterdatei für ein Gitter mit 9 Knotenpunkten beinhaltet folgende Werte:
| d | |
| 9 | |
| 0 | 0.0 |
| 1 | 0.125 |
| 2 | 0.25 |
| 3 | 0.375 |
| 4 | 0.5 |
| 5 | 0.625 |
| 6 | 0.75 |
| 7 | 0.875 |
| 8 | 1.0 |
| 0 | 0.125 |
| 1 | 0.125 |
| 2 | 0.125 |
| 3 | 0.125 |
| 4 | 0.125 |
| 5 | 0.125 |
| 6 | 0.125 |
| 7 | 0.125 |
und das Programm gibt diese Graphik aus:
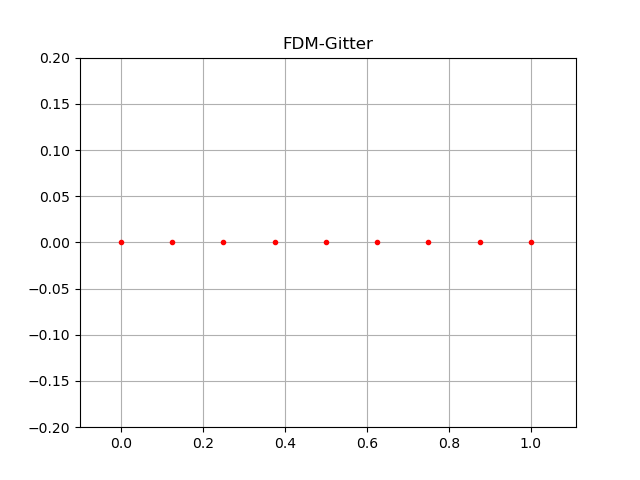
und speichert sie ab. Sie entspricht der FDM-Graphik oben.
Ein Gitter für FVM-Simulationen beinhaltet mehr, da neben den Gitterpunkten auch die Positionen der Grenzflächen und deren Flächeninhalte gespeichert werden müssen.
| v | |
| 10 | |
| 0 | 0.0 |
| 1 | 0.0625 |
| 2 | 0.1875 |
| 3 | 0.3125 |
| 4 | 0.4375 |
| 5 | 0.5625 |
| 6 | 0.6875 |
| 7 | 0.8125 |
| 8 | 0.9375 |
| 9 | 1.0 |
| 0 | 0.0625 |
| 1 | 0.125 |
| 2 | 0.125 |
| 3 | 0.125 |
| 4 | 0.125 |
| 5 | 0.125 |
| 6 | 0.125 |
| 7 | 0.125 |
| 8 | 0.0625 |
| 0 | 0.0 |
| 1 | 0.125 |
| 2 | 0.25 |
| 3 | 0.375 |
| 4 | 0.5 |
| 5 | 0.625 |
| 6 | 0.75 |
| 7 | 0.875 |
| 8 | 1.0 |
| 0 | 1.0 |
| 1 | 1.0 |
| 2 | 1.0 |
| 3 | 1.0 |
| 4 | 1.0 |
| 5 | 1.0 |
| 6 | 1.0 |
| 7 | 1.0 |
| 8 | 1.0 |
| 0 | 0.125 |
| 1 | 0.125 |
| 2 | 0.125 |
| 3 | 0.125 |
| 4 | 0.125 |
| 5 | 0.125 |
| 6 | 0.125 |
| 7 | 0.125 |
| 0 | 0.125 |
| 1 | 0.125 |
| 2 | 0.125 |
| 3 | 0.125 |
| 4 | 0.125 |
| 5 | 0.125 |
| 6 | 0.125 |
| 7 | 0.125 |
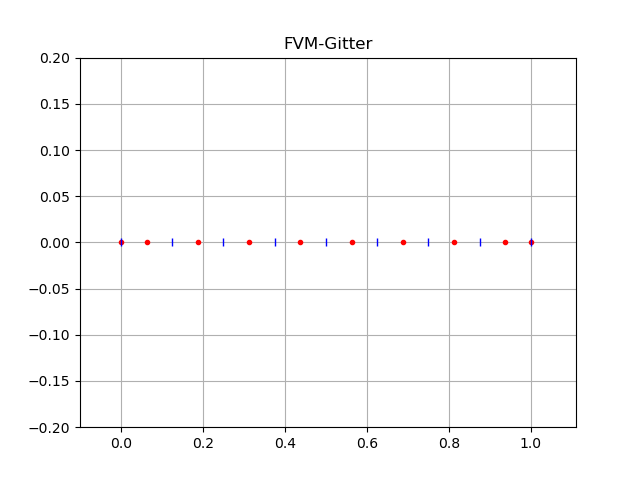
Die Knoten sind hier wieder durch rote Punkte, die Grenzflächen durch kleine blaue Striche gekennzeichnet.
|
|
 Who dares wins!
Who dares wins! 
 Who dares wins!
Who dares wins!