Korrelationskoeffizient_2

Auf dieser Seite wird die Reaktion des Korrelationskoeffizienten auf Phasenverschiebungen zweier Größen untersucht. Viele Vorgänge in der Natur hängen zusammen (z.B. Tagesverlauf des Sonnenscheines und der Bodentemperatur), weisen aber einen Zeitverzug auf (das Tagesmaximum des Sonnenscheines liegt bei 12:00 Uhr, während das Temperaturmaximum um 14:00 oder später erreicht wird, die Wärmeenergie muß sich erst akkumulieren).

Benutzung des Programms

1. Zuerst erstellen Sie ein Verzeichnis, in dem Sie das Programm "Korrelationskoeffizient" laufen lassen wollen.
2. In diesem Verzeichnis benötigen Sie alle Quelldateien und die Datei "steuer.txt". Am einfachsten ist es, das *.tar-Archiv herunterladen und im Zielverzeichnis zu entpacken. Das Archiv enthält die 4 Quelldateien, die Steuerdatei sowie die Dokumentation des Programms. als *.pdf. Sie können aber auch jede Datei einzeln herunterladen. Dann müssen Sie jeweils den Punkt - also "." - im Dateinamen vor py ergänzen. Sie müssen also die Dateinamen von "korrelations_koeffizient_haupt_2py" in "korrelations_koeffizient_haupt_2.py", "steuerpy" in "steuer.py", "rechnerpy" in"rechner.py" und "ausgabepy" in "ausgabe.py" ändern. Leider war es nicht möglich, die funktionierendem Dateiendungen beizubehalten, da der Server eine Fehlermeldung beim Anklicken ausgibt. Im *.tar-Archiv sind alle Dateiendungen richtig, die Programme sind sofort nach dem Entpacken lauffähig.
3. Dann öffnen Sie ein Konsolenfenster in diesem Verzeichnis (rechter Mausklick im Fenster des Verzeichnisses, dann "Terminal hier öffnen" klicken).
4. Führen Sie einen Virenscan über dieses Verzeichnis durch. Z.B. ich benutze clamscan mit dem Befehl clamscan -r -i. Sie können natürlich einen anderen Virenscanner benutzen.
5. Mit python3 korrelations_koeffizient_haupt_2.py startet man das Programm in der Konsole.
6. Die Eingabedaten befinden sich in der Datei "steuer.txt", sie müssen nicht mit der Tastatur eingegeben werden. Sie werden nach dem Programmstart sofort in einer Messagebox ausgegeben.
7. Nach einem Klick auf den "Weiter-"Button wird die Rechnung gestartet. Die berechneten Werte werden in der Konsole angezeigt, gleichzeitig werden zwei Ausgabedateien erstellt, eine mit den berechneten Korrelationskoeffizienten, eine mit den beiden Zufalls- und den beiden Sinusreihen.
8. Hier wird das Graphikmodul "matplotlib" benutzt. Nach dem Start des Programms, dem Anzeigen der Steuerdaten und dem Klick auf den "Weiter-"Button erscheint eine Graphik, die die Zufallszahlen als Punkte darstellt. Diese Graphik wird dann auch als .jpg gespeichert. Nach einem linken Mausklick auf das Kreuz rechts oben verschwindet diese Graphik und eine mit den beiden Sinusfunktionen erscheint, die wiederum abgespeichert wird.

Ergebnisdiskussion

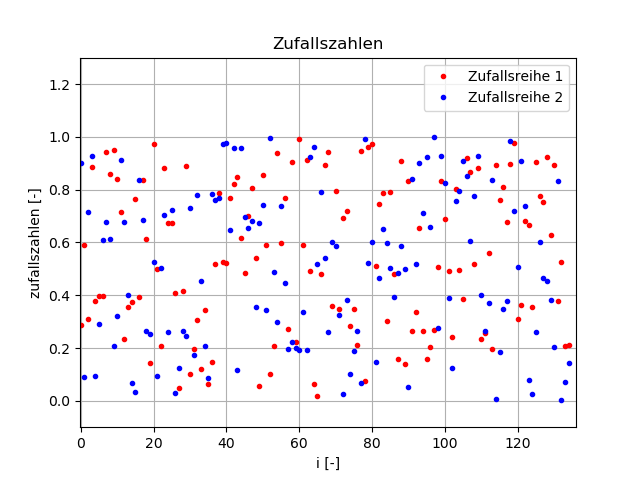
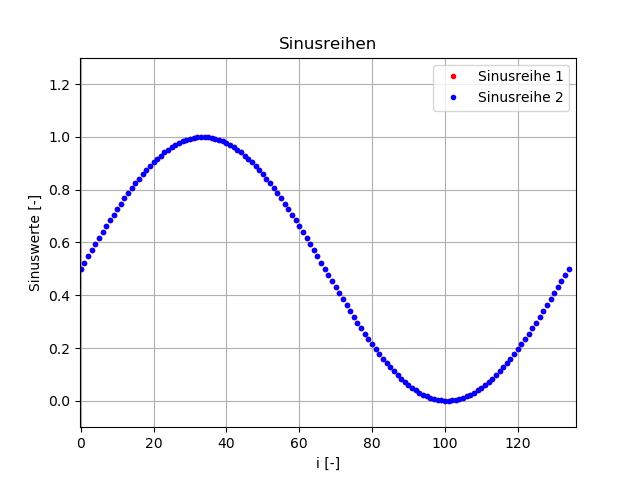
Das Programm errechnet den Korrelationskoeffizienten der Zufallsreihe. Bei einem Testlauf kam -0.03 , eine Zahl nahe 0 heraus, während die Sinusreihe einen Korrelationskoeffizienten von 1.0hat. Dieses gibt den Eindruck der Graphiken wieder: die Zufallszahlen bilden eine unzusammenhängende Wolke, während die Sinusfunktionen aufeinander liegen. Die Korrelationskoeffizienten werden beim Programmlauf im Terminal angezeigt und in die Datei "korr_phi_0.dat" eingetragen.

Was passiert, wenn die Sinusfunktionen eine Phasenverschiebung haben?

1. wird die Steuerdatei in einem Editor wie gedit geöffnet.
2. Unter dem Wort Phasenverschiebung_phi_[°] wird die 0.0 in z.B. 45.0 geändert.
3. Die Phasenverschiebung zwischen den beiden Sinusfunktionen ist dann +45°
4. Damit nicht die schon vorhandenen Ergebnisdateien "feld_ausgabe.dat" und korr.dat nicht überschrieben werden, müssen diese ebenfalls in der Steuerdatei geändert werden zu:
   • reihen_ausgabe_45.dat und
   • korr_45.dat
5. Ein weiterer Programmlauf, mit python3 korrelations_koeffizient_haupt_2.py gestartet, er wiederholt die Rechnung mit dem neuen Phasenwinkel 45°
6. Der Korrelationskoeffizient der Zufallszahlen liegt wieder nahe bei 0 - bei diesem Durchlauf 0.087, darum wenden wir uns gleich der phasenverschobenen Sinuszahlenreihe zu.

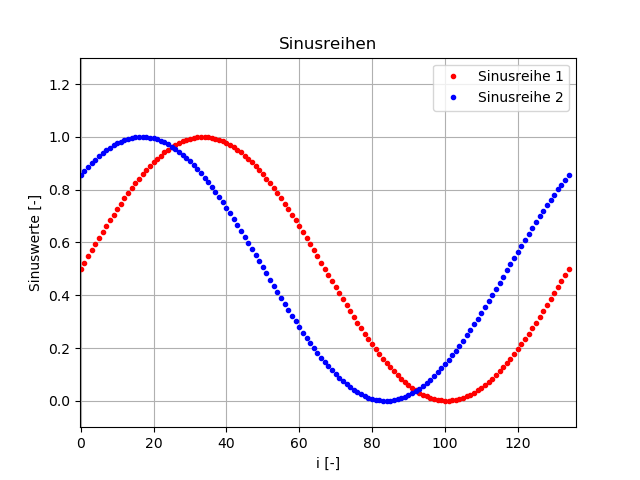
Ergebnisdiskussion

Die Sinusreihe einen Korrelationskoeffizienten von 0.705hat. Der Korrelationskoeffizient hat sich verringert.

Neue Phasenverschiebung 90°

1. öffnen wir die Steuerdatei im Editor
2. Unter dem Wort Phasenverschiebung_phi_[°] wird die 45.0 in 90.0 geändert.
3. Die Phasenverschiebung zwischen den beiden Sinusfunktionen ist dann +90°
4. Ein Überschreiben der bereits vorhandenen Ausgabedateien wird wieder verhindert, in dem die Dateinamen geändert werden zu:
   • reihen_ausgabe_90.dat und
   • korr_90.dat
5. Ein weiterer Programmlauf, mit python3 korrelations_koeffizient_haupt_2.py gestartet, wiederholt die Rechnung mit dem neuen Phasenwinkel 90°
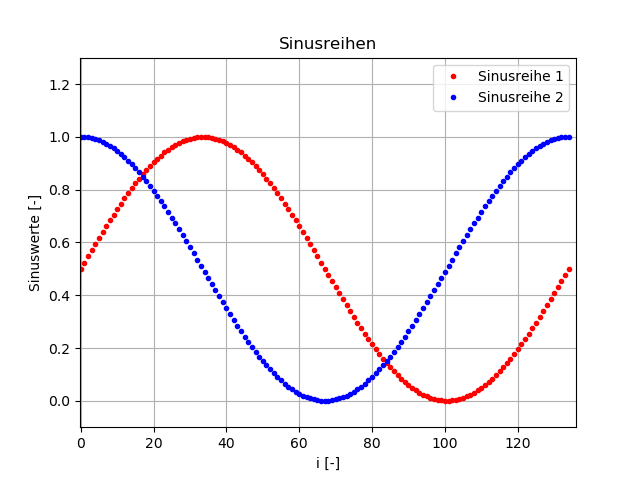
Während der Korrelationskoeffizient der Zufallszahlen einen Wert von -0.023 hat, ist der Korrelationskoeffizient der Sinusfunktionen 0.0 !

Autsch!

D.h. bei zwei phasenverschobenen aber sonst gleichen Funktionen kann der Korrelationskoeffizient den der Zufallszahlen unterschreiten, wenn die Phasenverschiebung ungünstig ist und die Zufallszahlen "nicht mitspielen"! Wir müssen also mit dem Korrelationskoeffizienten vorsichtig sein! Hier noch das dazugehörige Bild, erzeugt wie oben:



Dokumentation

Archiv python3

Hauptprogramm in python3

Steuereinheit in python3

Recheneinheit in python3

Ausgabeeinheit in python3

Steuerdatei

Zurück zur Startseite